Caractéristiques du nombre d’or
- Le nombre d’or, également connu sous le nom de ratio d’or, est un concept mathématique qui se réfère à un nombre irrationnel, approximativement égal à 1,618.
- Il est dérivé de la suite de Fibonacci, une série de nombres où chaque nombre suivant est la somme des deux nombres précédents.
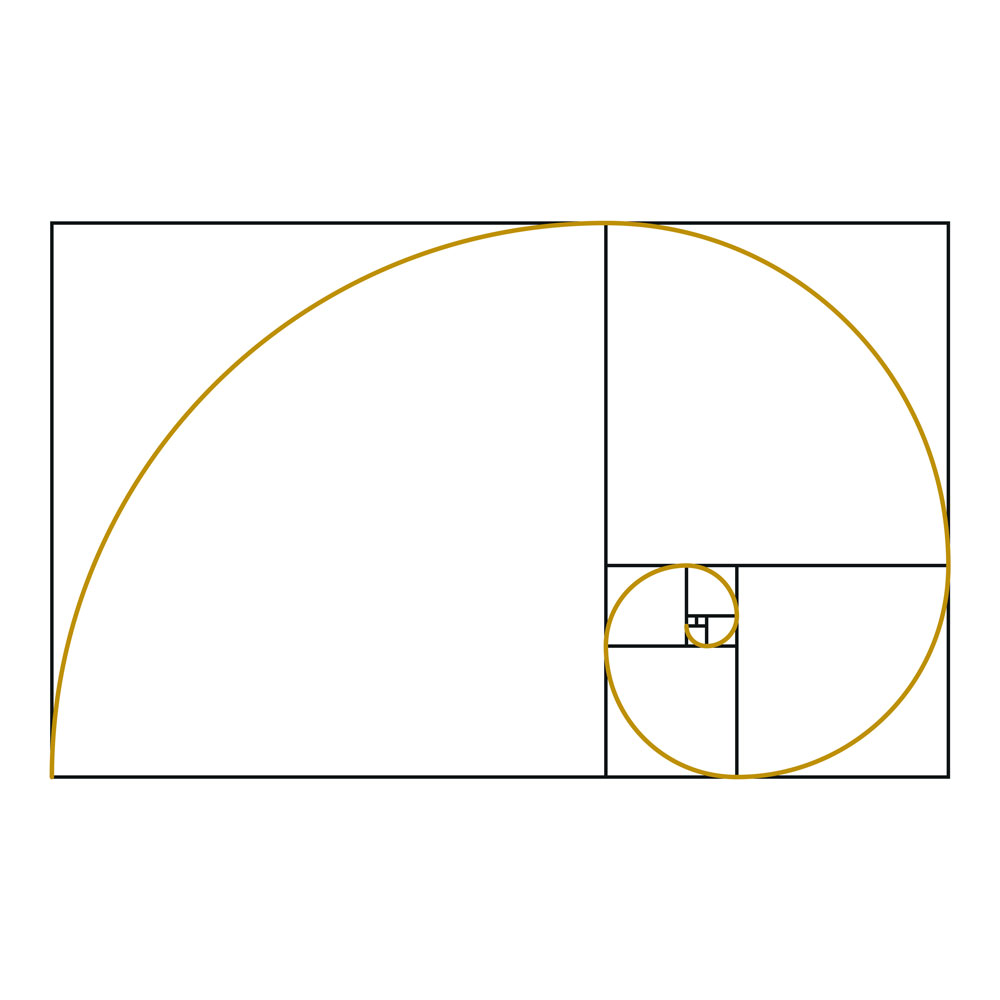
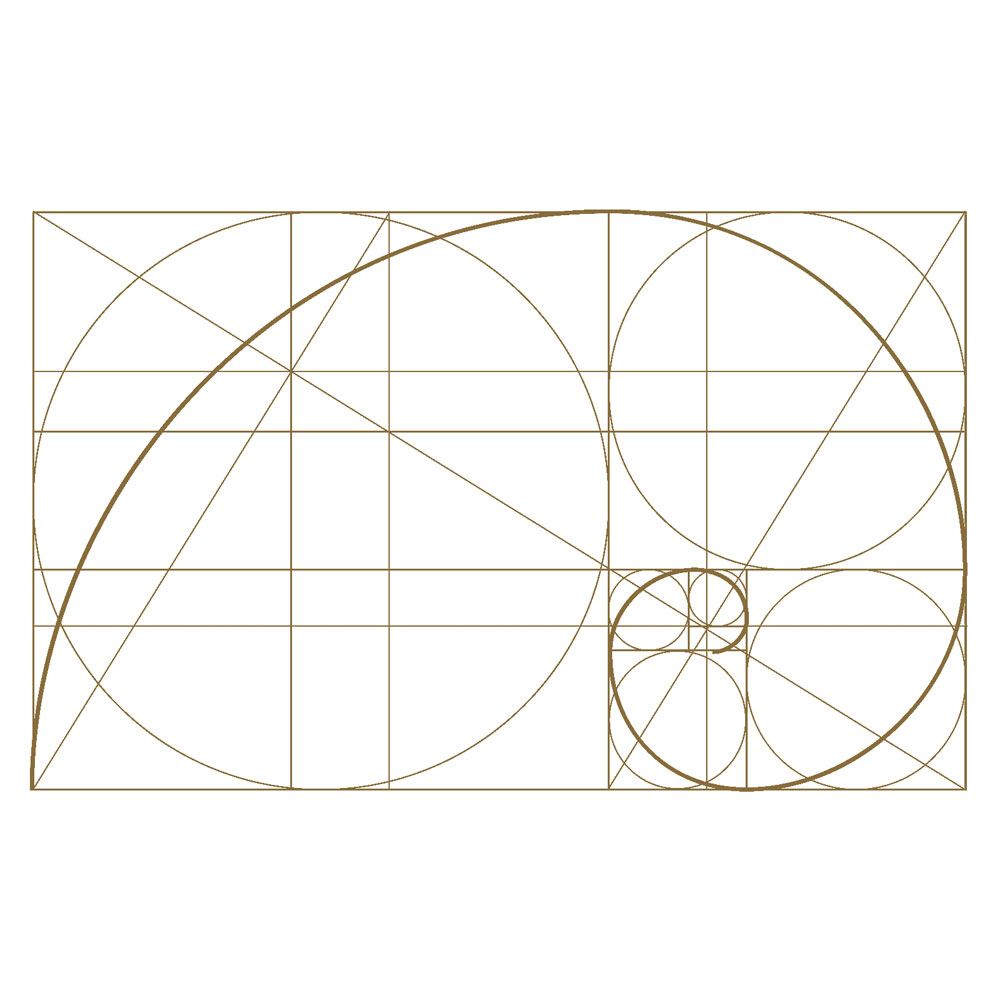
- Le ratio entre les deux parties est égal à 1,618. Il peut être utilisé pour créer un rectangle d’or ayant un rapport de 1,618 entre la longueur et la largeur.