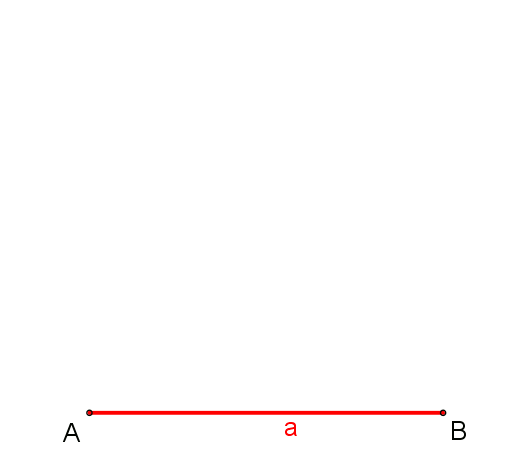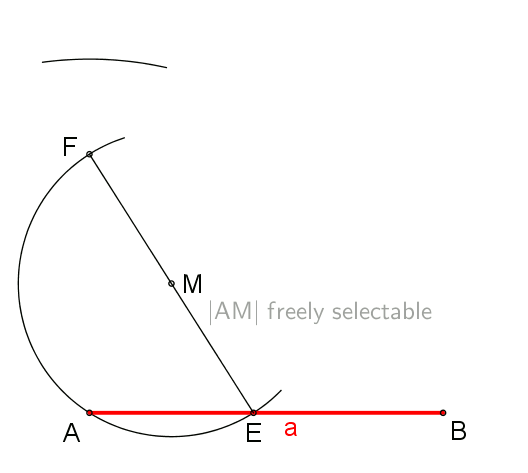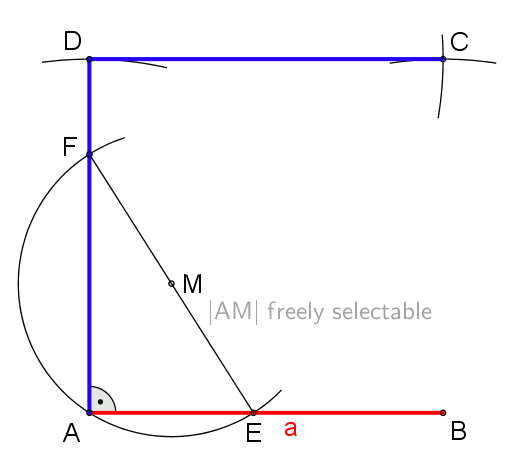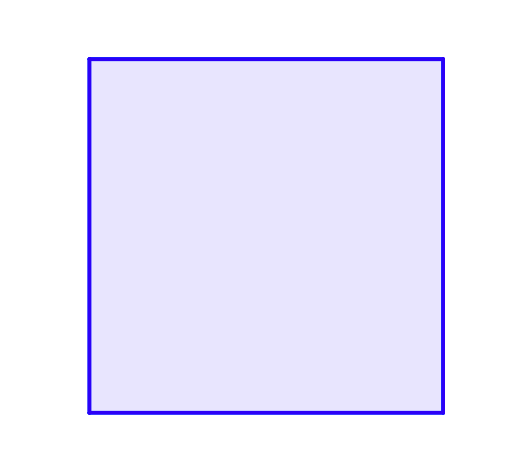
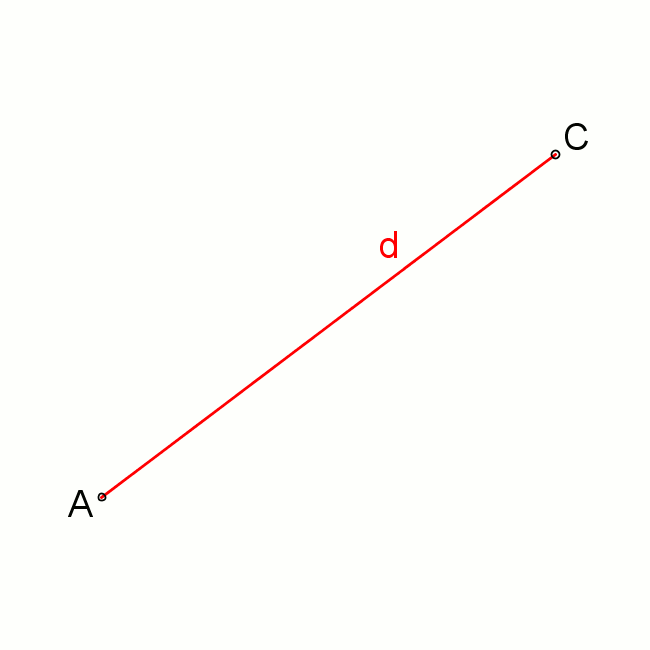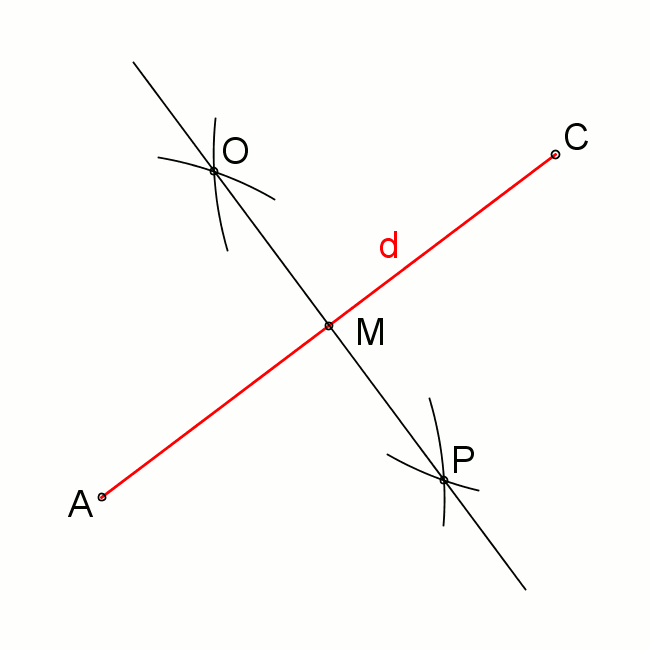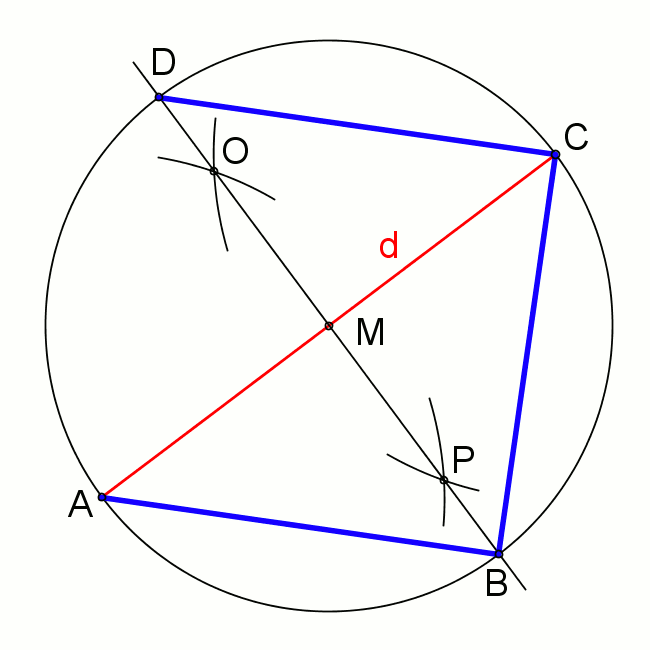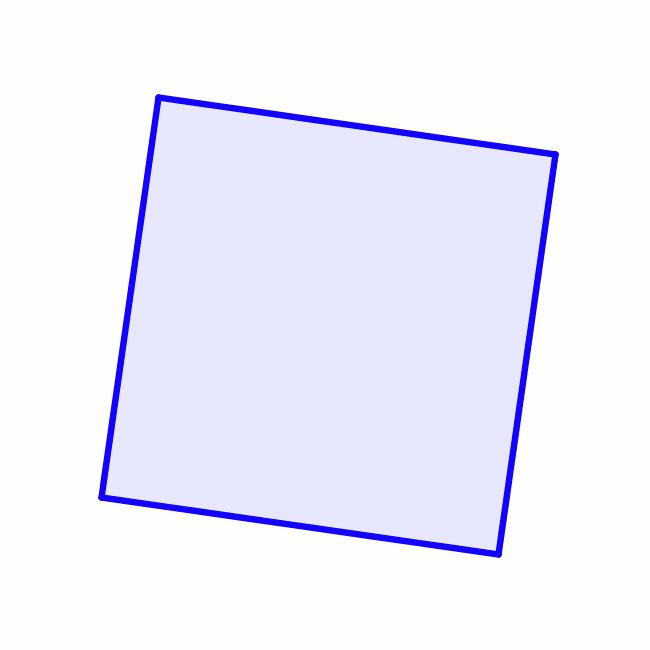
Caractéristiques du carré
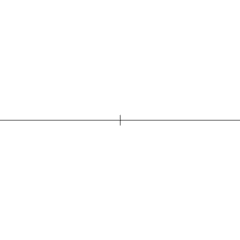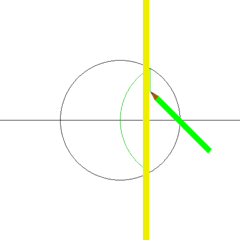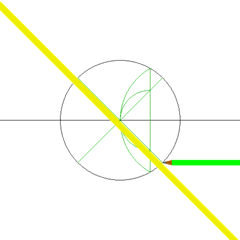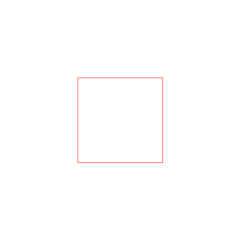
- Le carré est une figure géométrique définit comme un quadrilatère convexe, doté de 4 côtés de même longueur et 4 angles droits.
- Il appartient aux polygones réguliers (losange, rectangle, ou parallélogramme).
- Il a 4 symétries axiales, 2 rotations d’angles ainsi qu’une symétrie centrale.
- Ses premières représentations datent de la préhistoire.
- Le carré est l’une des figures géométriques les plus étudiées de l’antiquité.